All images © 2022 Chris Culy.
While working on a mathematical art project recently, I was struck by how many similarities there are between mathematical art and nature photography.
Mathematical art is art that is made by visualizing equations and formulas in an aesthetically pleasing way. The most well known type is fractal art, which became popular in the 1980s and 1990s, along with the spread of personal computers which let people make their own images. I experimented with it then, and I return to fractals and other mathematical art sporadically. One such foray was a series of small projects that were part of Fun with Zio Chris!. (The one project that wasn’t a fractal was Wall Drawing 256, which led, eventually, to Coloring Sol’s Walls.)
Recently I decided to revisit one of those fractals, the De Jong attractor. As I mentioned then, “Some things just call to you. When I first saw the De Jong attractor …, I knew that I would eventually create my own version. And I did.” Now I’ve made a second version, Exploring De Jong Attractors (=EDJA). Go ahead and check it out! But come back…
In thinking about what I like about the De Jong attractors, it occurred to me that there are lots of similarities between them (and mathematical art generally) and nature photography. There are two classes of similarities: aesthetic and non-aesthetic. One fundamental non-aesthetic aspect is that the mathematical objects exist and are available to be seen, just as nature exists and is available to be seen and photographed.1 (Click on the images to see them larger.)
Another non-aesthetic aspect is that the parameters of the mathematical art can be considered as analogous to geographical coordinates, to locations. For example, the parameters of the image above are a=1, b=-7, c=6, d=-1. The way I’ve written EDJA, you can click on this link to go directly to that “location”, visualized in a simple way:

These two images illustrate a few aesthetic parallels with (nature) photography. One parallel is the choice of color versus black and white. Art photography has long had a bias towards black and white, probably for historical reasons: until the 1910s or so, it was not easy to create color photographs. For mathematical art, there is no corresponding long-standing tradition, even though early home computers mainly did black and white.
Another parallel with photography is the appearance of “grain“, which has become one possible aesthetic choice in photography. With EDJA we can also choose to make “grainy” images (like the second one) or not.
The generalization is that with mathematical images, parallel to photography, we make choices in how we visualize the images.
Here’s another example:
The title of that image “Slipper” points to another similarity with nature (photography), and that is our tendency to see things in images (pareidolia), whether face, animals, or in this case, an object — a slipper, even when the image (or natural object) is clearly not what we imagine. In this case, the image is of points in the relevant De Jong attractor, a mathematical object, not a slipper.
This imagining of the image as a concrete object (a slipper) is in contrast to the more abstract images we saw previously. Nature photography also has both concrete and abstract forms. Concrete forms include landscapes, for example by the early woman photographer Elizabeth Withington, and “Il lago” (= “The lake”) by my friend Paolo Aldi. Abstract forms include many of Imogen Cunningham‘s plant images, like “Agave Design 2” and many of the images by Lia and Paolo Aldi in their “Sunny Flowers” series.
Here’s another image illustrating more similarities with nature photography:

The title of “3 against 2” suggests the polyrhythm of 3 beats against 2 (“triplets over duplets” in Wikipedia’s words). Here the visual image reminds us of an aural phenomenon, and we can find similar parallels in nature photography, where patterns might suggest sounds.
In addition in “3 against 2”, the foreground image is in shades of red, which is reminiscent of monochrome photographs, for example the early botanical cyanotypes by Anna Atkins.
Finally, as in nature, there is always something surprising, like this painterly image, which is very different from anything I’d seen before (and mostly since as well):

Another type of surprise could be a pattern across a series of locations. In the series “Hundreds” below, the c parameter of the location starts at -100 at the top left and decreases by 100 in each successive image, going left to right, top to bottom, while all other parameters are constant. In each image, the number of arcs corresponds (by a factor of -100) to the the c parameter. This was totally surprising to me. (Thanks to Lee McIntyre for the inspiration for this series.)
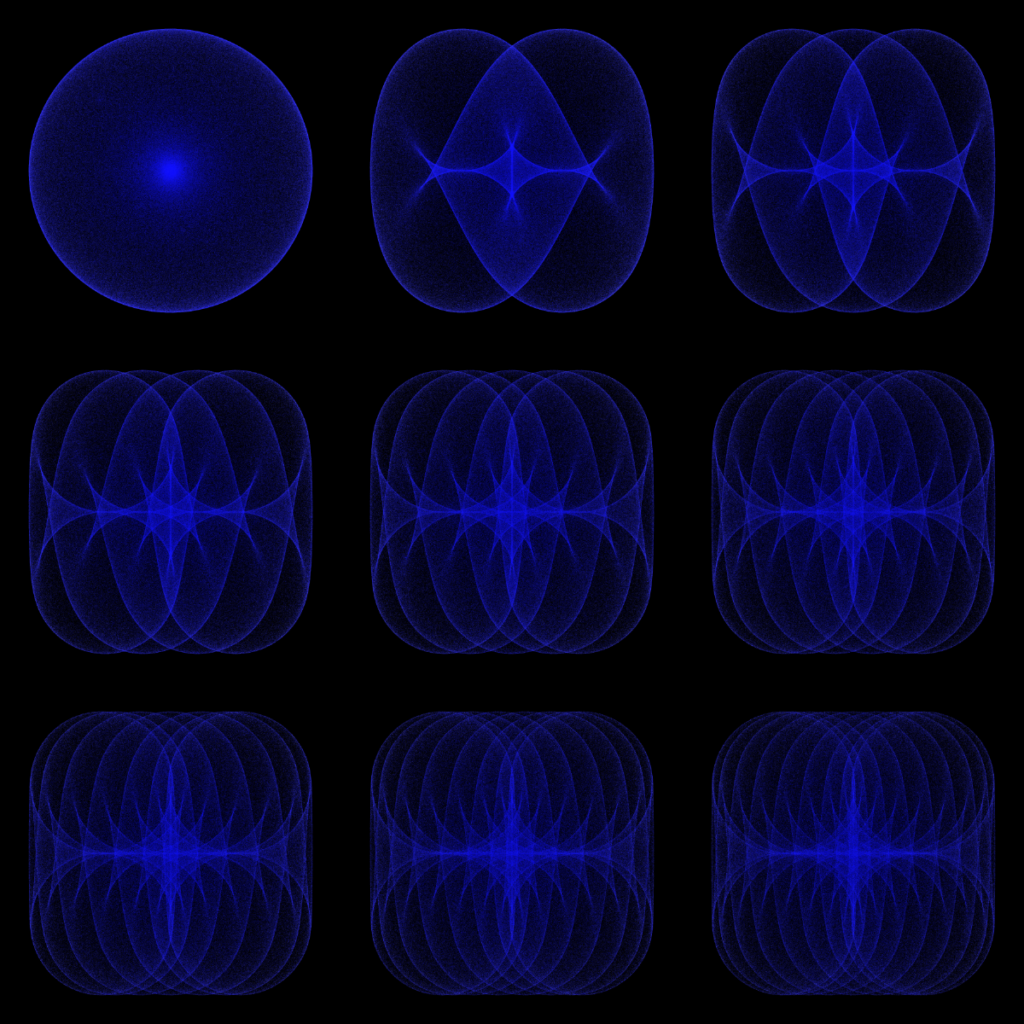
By the way, the “Hundreds” series shows yet another (simple) similarity between mathematical art and photography: we can combine separate images to form a montage. More generally, we can rework the original image in various ways. For example the initial image is cropped and rotated from the original.
In short, all of the artistry and skill that goes into nature photography also goes into mathematical art, from knowing the creative tools, to selecting the view, to creating the image. Add in patience and a bit of luck in finding good locations, and you truly have a parallel between mathematical art and nature photography.
Notes
1. This is a simple version of Platonic realism, which I’m happy enough not to think too deeply about.


